简单网格细分 1to4 Mesh Subdivision

Author Avatar
$H_P? Nov 27, 2018
  • Read this article on other devices

0x00 引言

最近搞研究要用到网格模型，算法要求输入任意一个mesh模型，输出的细分模型里面所有的mesh边长面积足够小，形状不变，法线不变。

0x01 现有算法

网格细分（Mesh Subdivision）已经很多现成比较好的算法，例如Loop算法，Catmull-Clark算法。详情参考文末附录，这里先不详述。

这两个算法的缺点是对于三维的模型，细分后都会改变原有模型形状，细分后的mesh法线也会发生变化和原来有不同。这就不符合使用要求了。

如图所示

LOOP

0x02 简单思路

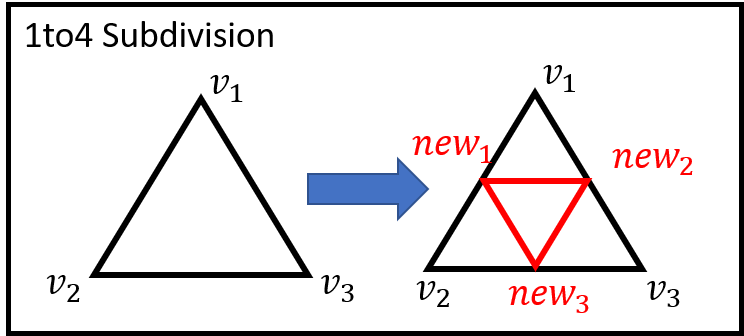
不考虑效率的情况下，简单一变四1to4细分网格的做法是：

  • 对每一个triangular mesh的每条边取中点形成新的顶点，然后分别连接相邻三个顶点形成新的细分三角形。

  • 细分后的四个三角形的法线和原来三角形一致。

scheme

0x03 MATLAB实现

利用stlread读取.stl格式的数据之后，得到f, v, n三个参数。

  • f是三列的数据，每列指代(indicate)每一个三角形的三个顶点。坐标记录在v里面。

  • v也是三列的数据，每列是每个顶点的x，y，z的坐标。

  • n也是三列的数据，每列是法线的方向向量。

%% created by H_P 20181119: subdivide mesh into 4 smaller meshes in a simple manner

function [Divided_faces, Divided_vertices, Divided_n]=MeshSubD1to4(facesLarge, verticesLarge, nLarge)

mesh_length_Large=length(facesLarge);  

Divided_faces=1:mesh_length_Large*4*3;
Divided_faces=(reshape(Divided_faces,[3,mesh_length_Large*4]))';
Divided_vertices=repelem(verticesLarge,4,1);
Divided_n=repelem(nLarge,4,1);

for n_for=1:mesh_length_Large
    new_1=(verticesLarge((n_for-1)*3+1,:)+verticesLarge((n_for-1)*3+2,:))/2;
    new_2=(verticesLarge((n_for-1)*3+3,:)+verticesLarge((n_for-1)*3+2,:))/2;
    new_3=(verticesLarge((n_for-1)*3+1,:)+verticesLarge((n_for-1)*3+3,:))/2;

    Divided_vertices((n_for-1)*12+2,:)=    new_1;
    Divided_vertices((n_for-1)*12+3,:)=    new_3;

    Divided_vertices((n_for-1)*12+4,:)=    new_1;
    Divided_vertices((n_for-1)*12+6,:)=    new_2;

    Divided_vertices((n_for-1)*12+7,:)=    new_2;
    Divided_vertices((n_for-1)*12+8,:)=    new_3;

    Divided_vertices((n_for-1)*12+10,:)=    new_1;
    Divided_vertices((n_for-1)*12+11,:)=    new_2;
    Divided_vertices((n_for-1)*12+12,:)=    new_3;

end

end

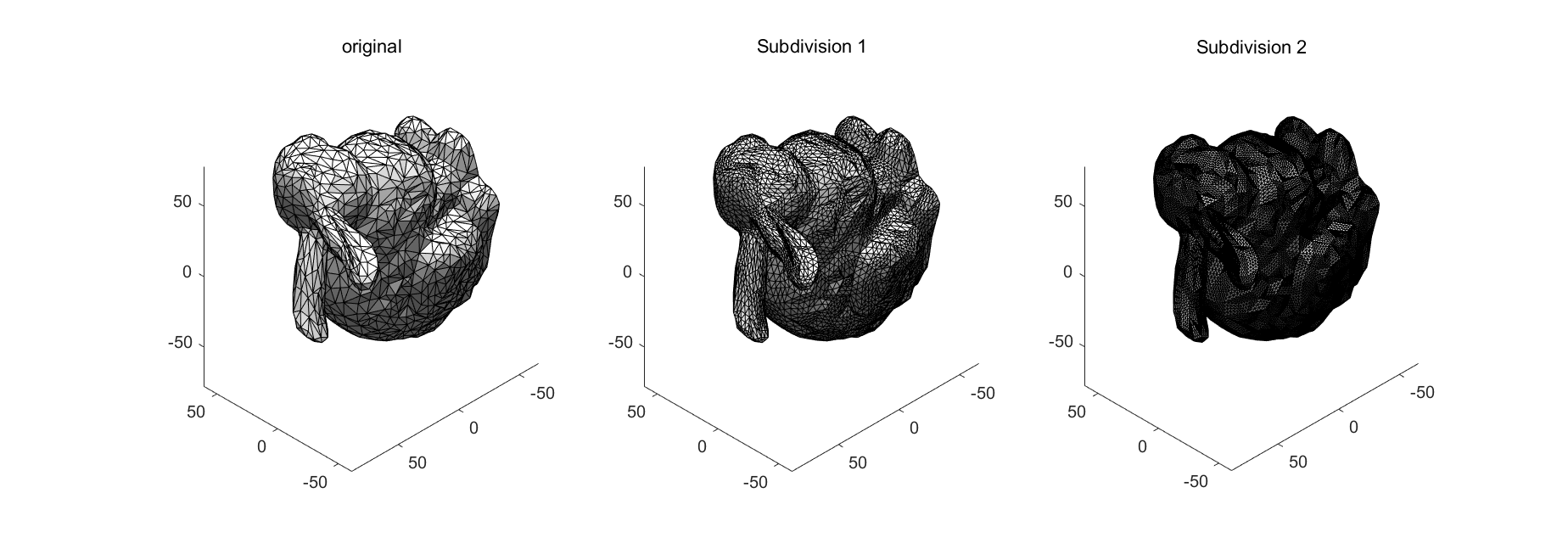
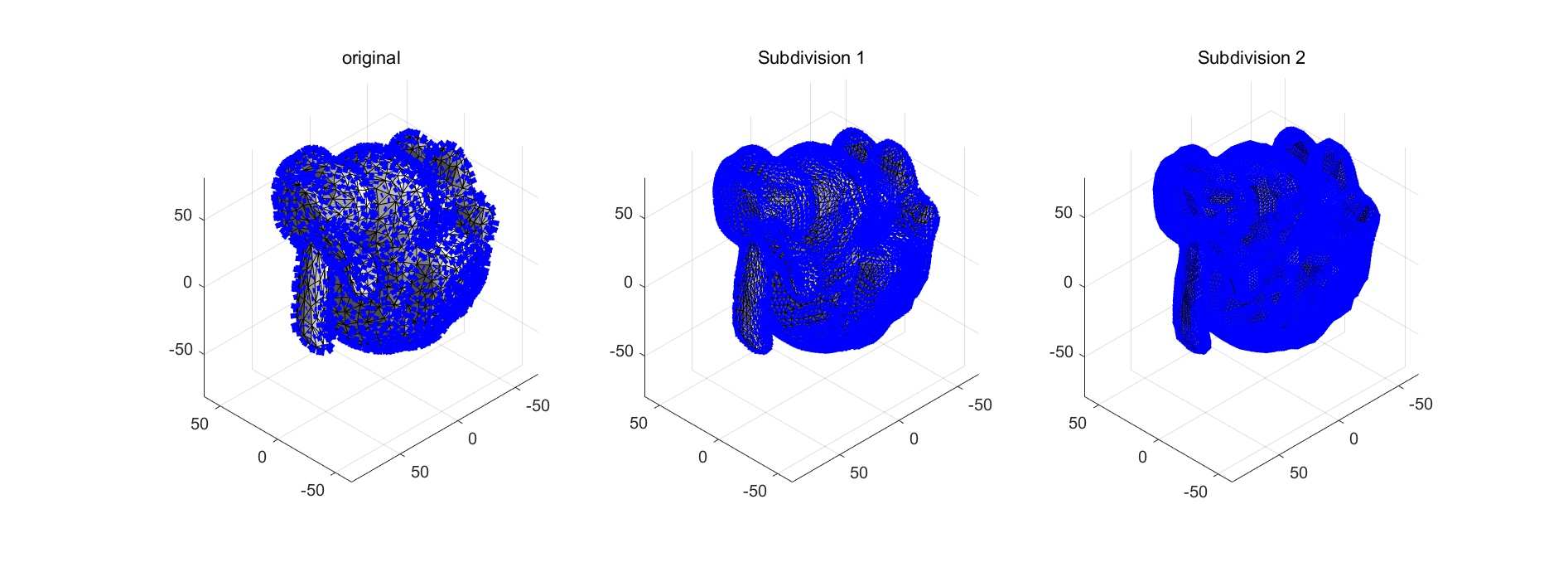
效果如图，细分后没有改变原来形状和法线。

comp1
comp2

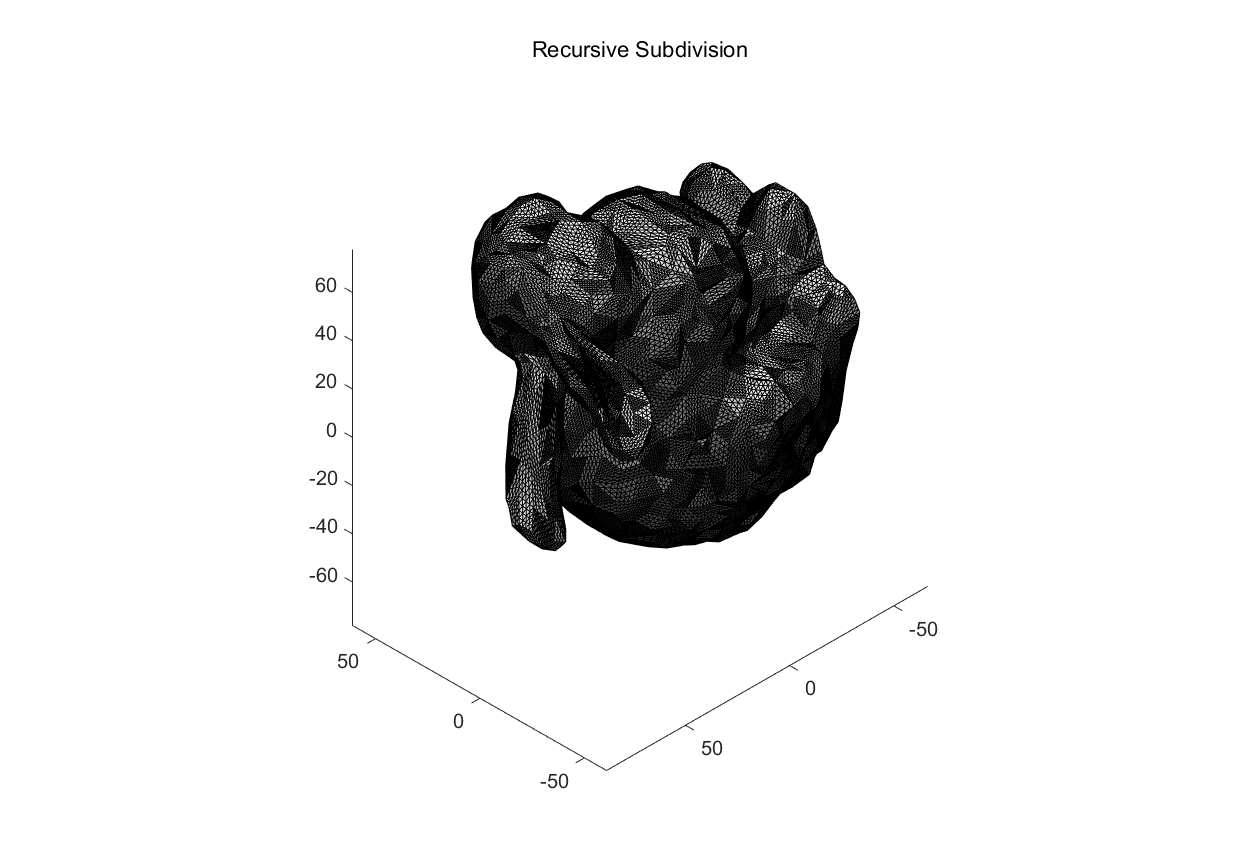
0x04 递归细分

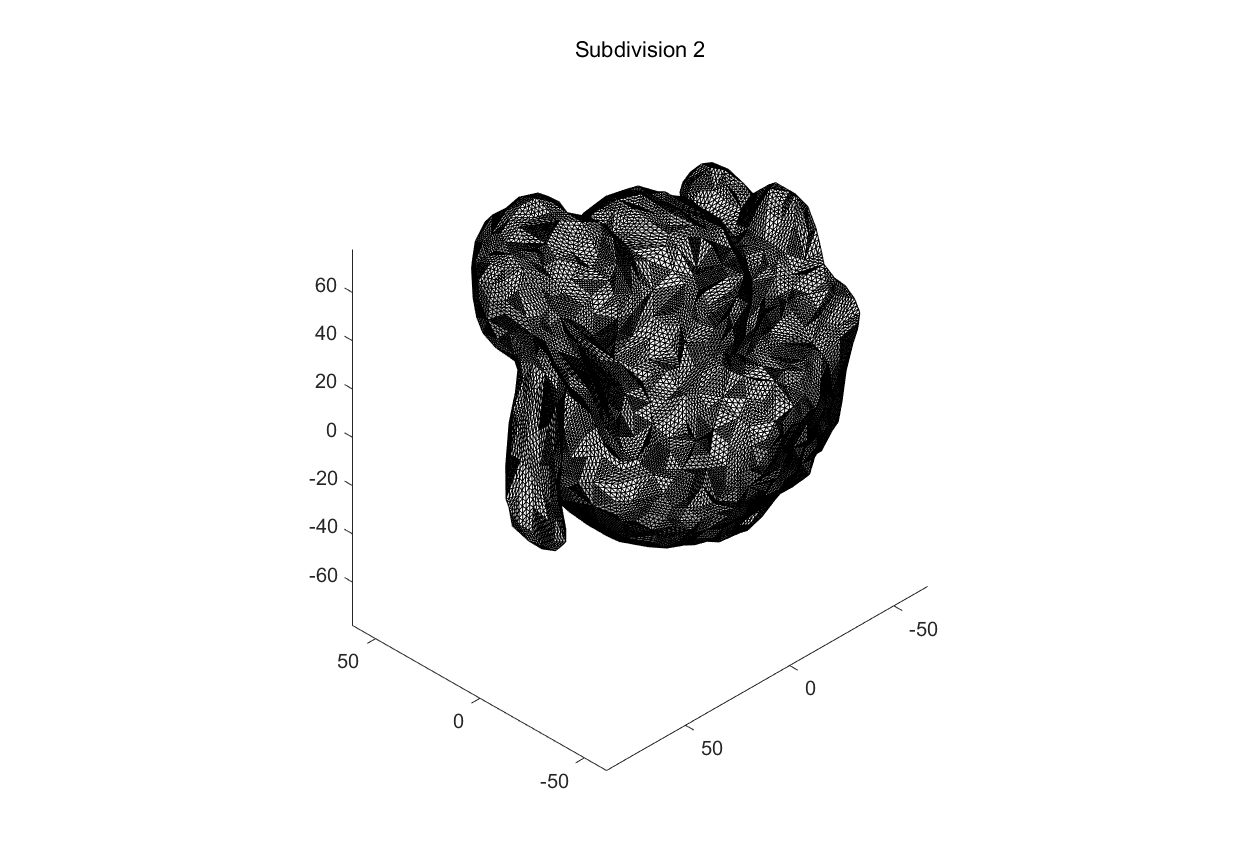
一般情况下，输入模型的各个mesh的大小是不规则的话，则需要不停寻找过大的mesh并进行细分，这时候使用递归算法效率高些。

SubD2
SubDRe

0x05 参考&其他

A Quick Introduction to Subdivision Surfaces

STLA_IO Read and Write Routines ASCII STL 3D Graphics Files

MATLAB将数据写入obj文件

matlab实现loop细分

渐进插值的LOOP 曲面细分

几个loop细分的例子

三维模型的网格细化

三维网格细分算法（Catmull-Clark subdivision & Loop subdivision）附源码

OpenGL 网格细分算法 Loop Subdivision - 附我的实现结果

վ HᴗP ի

This blog is under a CC BY-NC-SA 3.0 Unported License
Link to this article: https://hanspond.github.io/2018/11/27/简单网格细分 1to4 Mesh Subdivision/